Riffing on Le Guin's Carrier Bag Theory of Fiction, this presents a primordial vision of computation in which programs are written as a list of changes in the content of a bag, and programming can be done entirely without the need for textual representations.

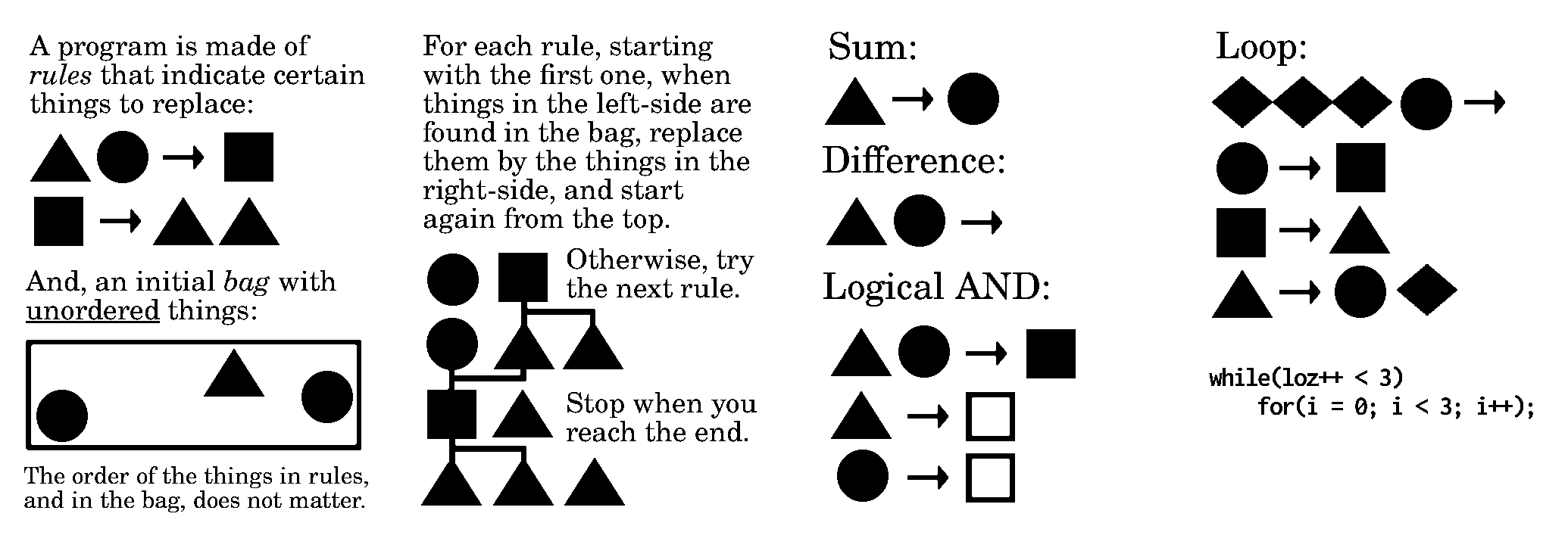
Programming is done by dragging things from the Panel(left) into the Rules(middle) or Bag(right). Step through the evaluation by pressing the button with the squiggly symbol(bottom right) to rewrite the symbols in the Bag

Click on the symbols in the Panel(left) to open the Symbol Editor with which you can draw new symbols, lock/unlock the dragging of the symbol in the bag, activate continuous/step mode for when the symbol is clicked on.

Clicking inside the bag during symbol editing gives that symbol an anchor position, when that symbol will be created as the result of a rule, it will spawn at that location.

To learn more, see the examples from Pocket Rewriting, and Fractran.
Questions? Join us on Discord

More information

Published	1 day ago
Status	Released
Platforms	HTML5
Rating	Rated 5.0 out of 5 stars (1 total ratings)
Author	Rek & Devine

Download

Download NowName your own price

Click download now to get access to the following files:

tote.rom 8.3 kB

Version 6

Comments

CoronaVitae44 minutes ago

Super cool. An obvious next step would be to make an import and export function so we can share things we've created (by which I mean smarter people can share and I can try them out).

Rek & Devine1 day ago

Wondering how to do arithmetic? Here's how to get the difference between two numbers:

:: x y sub > sub 
:: x   sub > sub pos 
::   y sub > sub neg 
::     sub >

Rek & Devine1 day ago

Here are some logic operations:

:: x y gth > gth 
:: x   gth > true 
::     gth > false  
:: x y lth > lth 
::   y lth > true 
::     lth > false  
:: x y equ > equ 
:: x   equ > false 
::   y equ > false
::     equ > true  
:: x y neq > neq 
:: x   neq > true 
::   y neq > true 
::     neq > false

Rek & Devine1 day ago

Here are some logic gates:

:: x y and > true 
:: x   and > false 
::   y and > false 
::     and > false  
:: x y or > true 
:: x   or > true 
::   y or > true 
::     or > false  
:: x y xor > false 
:: x   xor > true 
::   y xor > true 
::     xor > false  
:: true  not > false 
:: false not > true

Tote

Download

Comments